Kurvendiskussion von der Dachfunktion

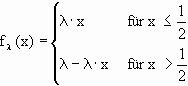
Definition der Dachfunktion

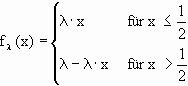	Die Dachfunktion besteht aus zwei linearen Teilen.

Nullstellen: x = 0 und x =1

Graphen: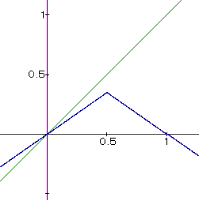
                       für l = 0,7

1. Ableitung: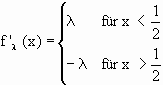

Þ Die Spitze hat den Wert

Fixpunkte:

Bei Fixpunkte gilt: f(x) = x x = lx Þ x (1-l ) = 0 Þ x = 0 ist die 1. Lösung, außer l = 1, dann sind alle x-Werte jeweils ihr Fixpunkt. x = l- lx Þ x (1+l) = l Þ x = ist die 2.Lösung. Es gibt die Fixpunkte z1 = 0 für x £ und z2 = für x >

• 0 < l < 1

für l<1 ist f'(z₁) < 1 Þ z₁ ein Attraktor
für l<1 ist z_{2 =} , x < Þ kein Fixpunkt

Spezial Fall: Für x₀ = 1 ist f(1) = 0, f(0) = 0, dies bedeutet, daß nach einer Iteration der Wert fest bleibt ( Fast-1-Fixpunkt ).

Beispiel:

Bei diesem Beispiel ist l = 0,7 und die zwei Startwerte sind x₁ = -0,4; x₂ = 0,4.

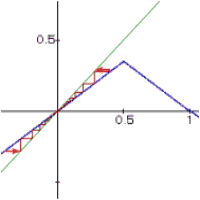	x1 und x2 streben gegen 0

• l = 1

für ein l = 1 ist jeder x-Wert £ ein Fixpunkt. Jeder x-Wert > ist ein Fast-1-Fixpunkt und bleibt nach der der 1. Iteration fest.
für x > :   f (x₀) =1-x₀ <, f² (1-x₀) = 1-x₀

Beispiel:

Bei diesem Beispiel ist l = 1 und die zwei Startwerte sind x₁ = 0,6; x₂ = 0,8.
f(x₁)=1-0,6 = 0,4
f(x₂)=1-0,8 = 0,2

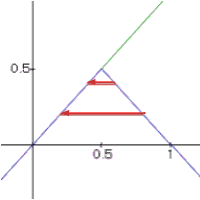	x1 strebt gegen 0,4; x2 strebt gegen 0,2;

Nun wird nur noch der Bereich von 0 £x₀£1 betrachtet, da die Folge für x<0 und x>1 gegen ¥ strebt und somit nicht interessant ist.

• 1 < l £ 2

Bei der Untersuchung von höhren Perioden erhält man weitere Fixpunkte:

Fixpunkte:

Bei Fixpunkte der zweiten Periode gilt: f l (x) ¹ x und f l (f l (x)) = x für x0 £ : x0 = l²x0 Þ x0 (1-l² ) = 0 Þ x = 0, keine Lösung im Definitionsbereich; 1-l² ¹ 0, da l >1 ist ( keine Fixpunkte ). Nach der 1.Iteration kann l0x > sein. Dann gilt: f l (f l (x0)) = l- l²x0 Aus x0 = l- l²x0 Þ x0(1+l²) = l Þ x0 = x0 = ist < im Bereich von 1<l£2. Nach der nächsten Iteration des Fixpunktes gilt: f() = l = Es gibt genau einen echt 2-periodischen Fixpunktpaar der 2. Ordnung: , Echter Fixpunkt einer beliebiger Ordnung: Es lassen sich weitere Fixpunkte finden, indem man die n-te Iteration von f betrachtet und auf Fixpunkte untersucht.

Beispiel:

Bei diesem Beispiel ist l = 1.5 und daraus ergibt sich einen Startwert 6/13 für den Fixpunkt der zweiten Periode. Nach der Iteration ergibt sich der Wert 9/13.

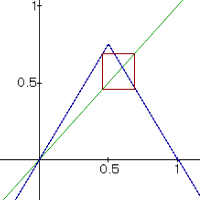	x Pendelt zwischen 6/13 und 9/13

Beispiel:

In diesem Beispiel ist l = 2.
Für die erste Iteration gilt: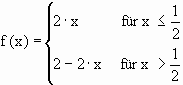
Die Fixpunkte sind z₁ = 0 und z₂ = 0.6666..

Bei der nächsten Iteration gibt es dann vier verschiedene Fälle:
1. Fall 2(2x) = 4x / 2. Fall 2-2(2x) = 2-4x / 3.Fall 2-2(2-2x) = -2-4x / 4. Fall 2(2-2x) = 4-4x

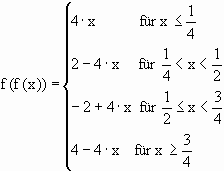
Die Fixpunkte sind z₁ = 0; z₂ = 0,4; z₃ = 0,666..; z₄ = 0,8

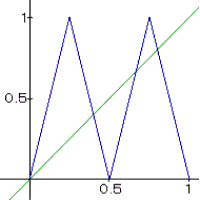
	f(x)	f(f(x))

Nun stellt sich heraus, daß die Winkelhalbierende jede Teilstrecke von f^k(x) genau einmal schneidet. Weil die n-te Iteration sich aus genau 2^k Teilstrecken zusammensetzt, gibt es 2^k Fixpunkte.

Cantor-Menge

Beispiel:

In diesem Beispiel ist l = 3.
Für die erste Iteration gilt: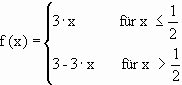

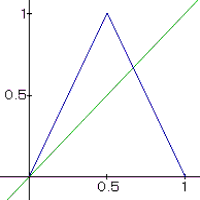
Graphen: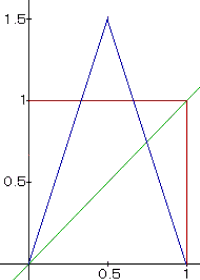
                       für l = 3
Nach der ersten Iteration der Menge 0 £x₀ £ 1, gibt es eine Menge für die gilt y > 1 und y < 0. Diese wird für die zweite Iteration ausgschloßen, da x₁ >1 ist und gegen ¥ strebt.

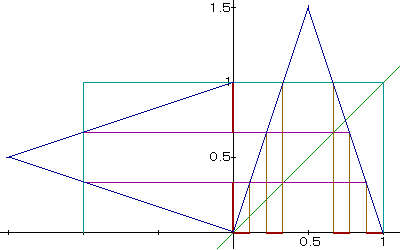	Auf der y-Achse werden die Werte der 1. Iteration aufgetragen, die nicht gegen ¥ streben. Es läßt sich dadurch graphisch die Startwerte auf der x-Achse der 2. Iteration ermitteln, die nach der 2. Iteration sich im Einheitsintervall befinden.

Setzt man die Iterationen bis ins Unendliche fort,. so bleibt die CANTOR - MENGE übrig.

Definition:	Man konstruiert eine Teilmenge des Intervalls [0,1] und entfernt im ersten Schritt das offene mittlere Drittel [1/3,2/3] von der Teilmenge [0,1], dabei erhält man [0,1/3] und [2/3,1]. Im zweiten Schritt wird aus den beiden Intervallen das mittlere Drittel entfernt.. So fortfahrend entsteht die Folge Ck mit C0, Ck+1= Ck\{offene mittlere Drittel}
Beobachtungen:	Ck besteht aus 2k abgeschlossenen Intervallen der Länge 3-k, die man als Ck-Intervalle bezeichnet und es gilt .
Gesamtlänge von C:	Für die Berechnung der Gesamtlänge einer Menge Ck multipliziert man die Anzahl der Intervalle mit der Länge: L(Ck) = 2k *3-k = (2/3)k.

Es gibt eine weitere Möglichkeit die Cantor-Menge darzustellen:

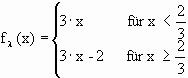Graphen: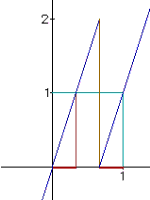
Nach einer weiteren Iteration ist die Funktion durch folgende Gleichung definiert:
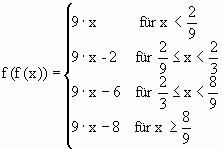Verallgemeinert man diese Funktion, dann kann man beliebige Cantor-Mengen erstellen:
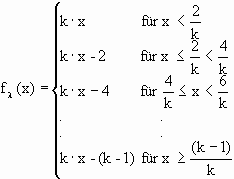