Nun kann eine Population nicht ewig ansteigen, da irgendwann ein Teil der Tiere nichts mehr zu fressen findet und dann wieder sterben. Dies muß durch ein Faktor
Der Forscher Holländer Verhulst suchte eine Formel für die Entwicklung
von Tierpopulationen. Die Tierpopulationen können entweder ein chaotisches
Verhalten zeigen, oder über hundert Millionen Jahre stabil sein, wie zum
Beispiel die Haie. Andere Arten wie die Saurier sterben plötzlich aus oder
wie die in Australien ausgesetzten Kaninchen vermehren sie sich schlagartig.
Lemminge haben einen Vier-Jahres-Rhytmus. Viele Populationen erscheinen dagegen
in ganz unregelmäßigen Abständen.
Verhulst vereinfachte das Model sehr stark, dabei betrachtet er eine Art die
nur von der Nahrungskette abhängt und nicht durch natürliche Feinde
bedroht ist. Man muß sich vorstellen, dass die Spezie auf einer verlassenen
Insel ausgesetzt wird. Weiterhin wird angenommen, dass die Population eines
Jahres nur von der Anzahl der Tiere im Vorjahr abfängt. Das geeignete Tier
für das Modell sind die Insekten, da sie alle Bedingungen erfüllen.
Sie leben im Sommer, legen ihre Eier und sterben später. Nächstes
Jahr schlüpfen aus den Eiern die nächste Generation. Wie lautet nun
die Gleichung?
1. Schritt:
Man braucht eine Variable m für die Nachkommen:
| zn = mza | zn die Anzahl der Tiere für das neue Jahr, za für das alte Jahr |
| Ist m<0 nimmt die Population
ab. Ist m>0 nimmt die Population zu. |
|
2. Schritt:
Nun kann eine Population nicht ewig ansteigen, da irgendwann ein Teil der Tiere
nichts mehr zu fressen findet und dann wieder sterben. Dies muß durch
ein Faktor ![]() berücksichtigt
werden. zm ist dabei ein Maximalwert der nie erreicht wird, da je
größer die Anzahl der Insekten wird, verringert sich der Faktor.
berücksichtigt
werden. zm ist dabei ein Maximalwert der nie erreicht wird, da je
größer die Anzahl der Insekten wird, verringert sich der Faktor.
![]()
3. Schritt:
Am Schluß teilte Verhulst beide Seiten durch zm. Das hat den
Effekt , dass ein Anteil ausgerechnet wird statt einer absoluten Zahl. ( Beispiel:
ein drittel der Deutschen tragen eine Brille statt 26,66 Millionen Deutsche
):
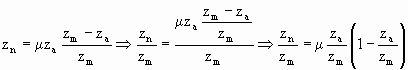
| f(x) = mx(1-x) |
f(x) = |
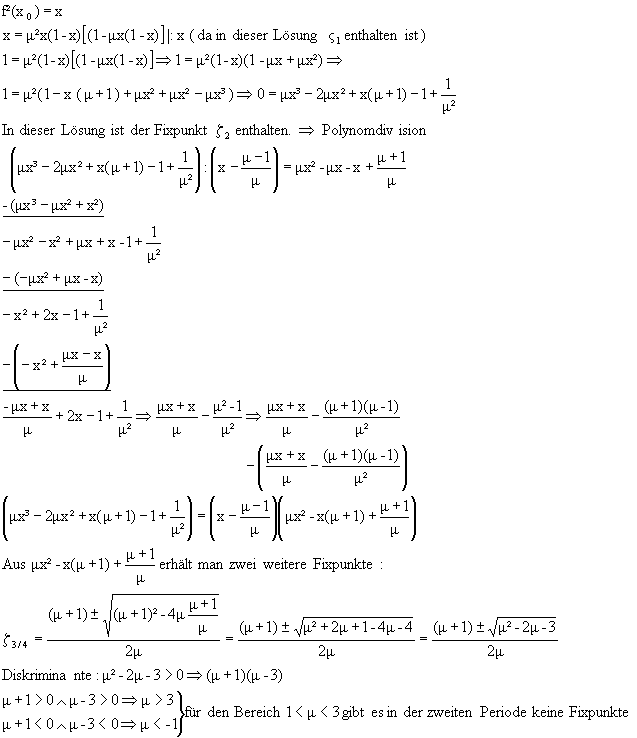
Das Feigenbaum-Diagramm kann man mit dem Computer aus der logistischen Funktion f(x) = mx(1-x) erstellen. Das Feigenbaum-Diagramm zeigt ab einen bestimmten Bereich ein chaotisches Verhalten.
Kurvendiskussion von f(x) = mx(1-x)Nullstellen: x = 0 und x = 1
Graphen: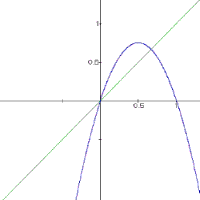
für
m = 3
1. Ableitung: f(x) = mx(1-x)
Þ f'(x) = m
-2mx f'(x) = 0
Þ x = 1/2
![]()
Die Funktion ist eine nach unten geöffnete Parabel.
| Fixpunkte: | Bei Fixpunkte gilt: f(x) = x x = mx(1-x) | : x ( x = 0 ist die 1.Lösung ) 1 = m(1-x) Þx = Es gibt nun zwei Fixpunkte: z1 = 0 und z2 = f'(z1) = m und |
für m<1 ist f'(z1)
< 1 Þ z1
ein Attraktor
für m<1 ist f'(z2)
> 1 Þ z2
ein Repellor
Der Einzugsbereich von z1 ist
von ![]() < x < 1-
< x < 1-![]() .
.
| für: | x < |
|
| x >1- |
Beispiel:
Bei diesem Beispiel ist m = 0,85 und die drei Startwerte sind x1 = 0,8; x2 = 1,1; x3 = 1,3. Daraus ergibt sich der Einzugsbereich von -0.1747 < x < 1.1764 für den Fixpunkt z1.
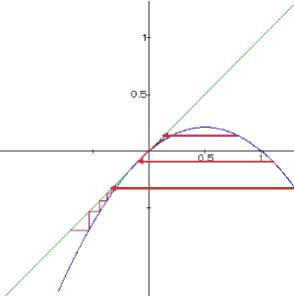 |
| x1 und x2 streben gegen 0 |
| x3 strebt gegen ¥, da x3 außerhalb des Einzugsbereich ist. |
Bei m = 1 existiert nur ein Fixpunkt, da der
Punkt z2 = ![]() in den Ursprung fällt.
in den Ursprung fällt.
Þf'(z1)
= 1
Der Einzugsbereich von z1 ist von 0
£ x £ 1
Für ein m
>1 sind alle interessante
x -Werte im Intervall [0,1].
Für alle x0 < 0 und x0 > 1 gilt ![]()
Für alle 0<x0 <1 gilt ![]()
Im Bereich 1< m< 3 gibt es genau zwei Fixpunkte
z1 und z2
, nämlich den Ursprung und den Punkt z2
.
für 1< m< 3 ist f'(z1)
> 1 Þ z1
ein Repellor , da gilt m >1
für 1< m< 3 ist f'(z2)
< 1 Þ z2
ein Attraktor, da |2- m| < 1 ist.
| 1.Fall: | 2-m > 0 Þ m < 2 daraus folgt: f'(z2) = 2- m < 1 für 1< m < 2 |
| 2.Fall: | 2-m < 0 Þ m >2 daraus folgt: f'(z2) = m-2 < 1 für 2< m < 3 |
| 3.Fall: | 2-m =0 Þ m = 2 daraus folgt: f'(z2) = 2- m = 0 < 1 für m = 2 |
Bei diesem Beispiel ist m = 2,3 und der Startwert x1 = 0,01. Daraus ergibt sich für z2 = 0,5652.
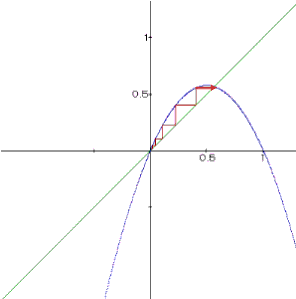 |
 |
|
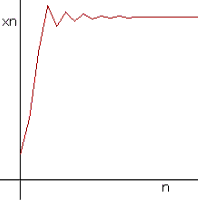
| x1 strebt gegen z2 | xn pendelt gegen den x-Wert des Fixpunktes bei zunehmender Iteration |
Die Fixpunkte der ersten Periode erweisen sich als abstoßen.
für m > 3 ist f'(z1)
> 1 Þ z1
ein Repellor, da gilt m >1
für m > 3 ist f'(z2)
> 1 Þ z2
ein Repellor, da |2- m| > 1 ist
Bei der Untersuchung der zweiten Periode erhält
man zwei weitere Fixpunkte:
f2(x) = f( f(x)) = m²x(1-x)[1-mx(1-x)]
= m2x(1-x)[1-mx(1-x)]
| Graphen: | 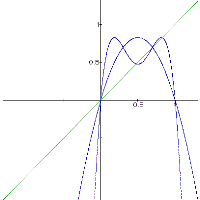 |
|
für m = 3 |
| 1.Ableitung: | f2(x) = m2x(1-x)[1-mx(1-x)]
=(m2x-m²x²)[1-mx+mx²)]
=m²x-m³x²+m³x³-m²x²+m³x³-m³x4
Þ f²'(x) =m²-2m²x-2m³x+6m³x²-4m³x³ = m²(-4mx³+6mx²-2mx-2x+1) ( Polynomdivision ) (-4mx³+6mx²-2mx-2x+1):(-2x+1) = 2mx²-2mx+1 -(-4mx³+2mx²) 4mx²-2mx-2x+1 -(4mx²-2mx) -2x+1 f²'(x) = m²(1-2x)(1-2mx+2mx²) |
| Fixpunkte: |
f2(x) = x |
Untersuchung der Fixpunkte:
|f²'( z3/4)| =
|m²-2 m-4|![]()
Nun wird überprüft für welches m
> 3 die Fixpunkte Attraktoren oder Repelloren sind.
Attraktoren: |m²-2
m-4| = |(m-1)²-5| < 1 Þ
|(m-1)²-5|-1 < 0
Repelloren: |m²-2
m-4| = |(m-1)²-5| >1 Þ
|(m-1)²-5|-1 > 0
Auflösen der Betragsstriche:
| 1.Fall: | (m-1)²-5 > 0 Þ
m > 1+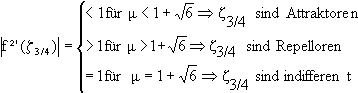
|
| 2.Fall: | (m-1)²-5 < 0 Þ
m < 1+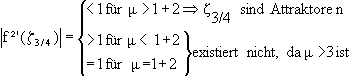 |
| 3.Fall: | (m-1)²-5
=0 Þ m
=1+ |f²'( z3/4)| = 0 < 1 Þz3/4 sind Attraktoren |
Zusammenfassung:
Im Bereich 3 <m < 1+![]() gibt es genau 4 Fixpunkte der zweiten Periode, nähmlich den Ursprung 0,
den Punkt x =
gibt es genau 4 Fixpunkte der zweiten Periode, nähmlich den Ursprung 0,
den Punkt x = ![]() und die Punkte
und die Punkte ![]() ,
wobei die Fixpunkte z1/2 abstoßend
sind und die Fixpunkte z3/4 anziehend
sind.
,
wobei die Fixpunkte z1/2 abstoßend
sind und die Fixpunkte z3/4 anziehend
sind.
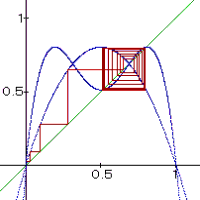
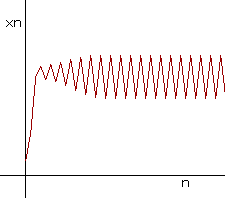
Beispiel:
Bei diesem Beispiel ist m = 3,2 und der Startwert
ist x1 = 0,01. Die Fixpunkte haben folgende Werte:
z2 = 0,6875 ist abstoßend
z3 = 0,513 ist anziehend
z4 = 0,8 ist anziehend
 |
 |
|
| x1 pendelt zwischen den beiden x-Werten der Fixpunkte z3/4 bei zunehmender Iteration | ||
Für ein m >1+![]() müssen anziehende Fixpunkte von höhren Perioden bestimmt werden. Die
dafür erforderlichen Rechnungen werden extrem aufwendig, die nur mit Hilfe
des Computers bestimmt werden können. Dabei kommt man zu dem Ergebnis,
daß es für f3(x) keine anziehenden Fixpunkte gibt ( im
Bereich 1 < m < m¥
). Erst f4(x) liefert 4 weitere Fixpunkte.
müssen anziehende Fixpunkte von höhren Perioden bestimmt werden. Die
dafür erforderlichen Rechnungen werden extrem aufwendig, die nur mit Hilfe
des Computers bestimmt werden können. Dabei kommt man zu dem Ergebnis,
daß es für f3(x) keine anziehenden Fixpunkte gibt ( im
Bereich 1 < m < m¥
). Erst f4(x) liefert 4 weitere Fixpunkte.
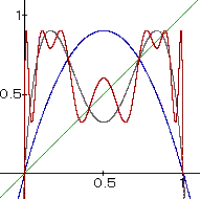
Beispiel:
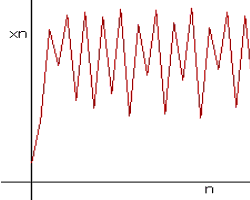
Bei diesem Beispiel ist m = 3,6 und es werden die Funktionen f(x,)f2(x),f4(x),xn dargestellt
 |
 |
|
| Xn pendelt zwischen den vier anziehenden Fixpunkte der 4 Periode hin und her. | ||
Nun wird das Koordinatensystem gewechselt, anstatt eines ( n,xn )-Koordinatensystems
wird ein ( m,xn )-Koordinatensystem
verwendet. Dies bedeutet, es werden alle xn-Werte der anziehenden
Fixpunkte in Abhängigkeit von m abgetragen.
Möglichst viele x-Werte werden aus [0,1] unendlich oft iteriert und der
dabei gefundene Grenzwert wird in einem Diagramm aufgetragen. Diesen realen
Grenzwert wird künfitg y genannt. Nach seinem Entdecker bezeichnet man
das ( m,y) - Diagramm als FEIGENBAUM. Der Einsatz
des Computers ist dabei unausweichlich.
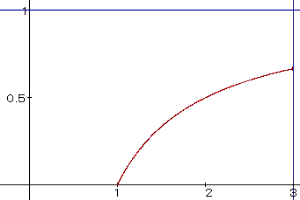
Das Feigenbaum - Diagramm:
In diesem Bereich gibt es einen anziehenden Fixpunkt z
= ![]() =
= ![]() und einen abstoßenden Fixpunkt, den Ursprung. Schreibt man z
=
und einen abstoßenden Fixpunkt, den Ursprung. Schreibt man z
= ![]() als Funktion y =
als Funktion y = ![]() ,
dann ist dies eine steigende Hyperbel mit dem Mittelpunkt (0,1). Die Asymptoten
haben die Gleichung m = 0 und
m=1.
,
dann ist dies eine steigende Hyperbel mit dem Mittelpunkt (0,1). Die Asymptoten
haben die Gleichung m = 0 und
m=1.
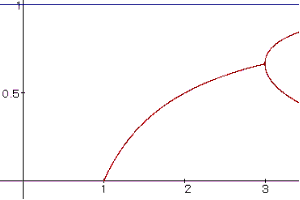
Für diesen Bereich gibt es zwei anziehende Fixpunkte, dabei kommt es zu einer
Aufspaltung des Hyperbelastes in zwei Teile. Dies ist eine Gabelung, anders
gesagt, eine Bifurkation oder eine Periodenverdoppelung.
Bei m =1+![]() kommt es zu weiteren Verdoppelungen, da die 4 Periode vier anziehende Fixpunkte
hat. Mit wachsendem m erscheinen immer neue
Verdoppelungen ( Kaskaden ), die immer näher zusammenrücken. Auch
die Abstände di der Gabelzinken nehemen ab. Mit dem Computer
lassen sich die Existenz zweier Grenzwerte nachweisen:
kommt es zu weiteren Verdoppelungen, da die 4 Periode vier anziehende Fixpunkte
hat. Mit wachsendem m erscheinen immer neue
Verdoppelungen ( Kaskaden ), die immer näher zusammenrücken. Auch
die Abstände di der Gabelzinken nehemen ab. Mit dem Computer
lassen sich die Existenz zweier Grenzwerte nachweisen:
Grenzwerte:
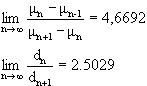
| Das Feigenbaum-Diagramm: | |
| Die Bifurkation kann man bis m¥ = 3.5699.. beopachten. Für ein größeres m springen die xn-Werte durcheinander, so lassen sich keine Vorhersagen mehr treffen. Dies wird als CHAOS bezeichnet. Die Bifurkationsphase stellt einen Übergang von der Ordnung zum Chaos dar. | |
|
|
|
| Wenn man das Feigenbaum-Diagramm genauer betrachtet entdeckt man innerhalb des Bereiches m¥<m < 4 hellere Streifen, Fenster. In diesen Fenster sind Brücken und wenn man diese Brücken vergrößert, ensteht ein neuer Feigenbaum. | |
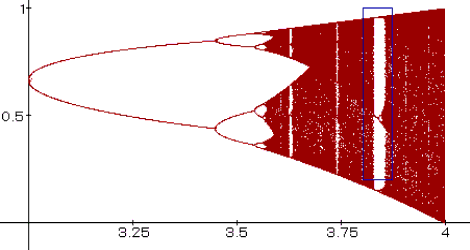 |
|
| Durch die Vergrößerung einer Brücke z.B. innerhalb des blauen Fensters ensteht ein neuer kleiner Feigenbaum. Dieser vergrößerte Feigenbaum hat den Bereich von 3,838<m < 3,8569. Nun könnte man wieder eine Brücke herausgreifen und vergrößern. Es ensteht also ein Blick ins UNENDLICHE. | |
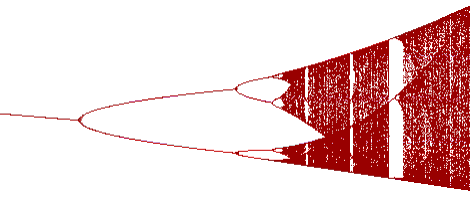 |
|
| x y |
|
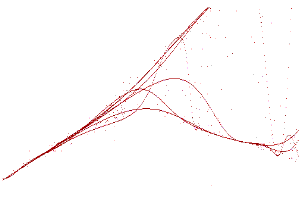 |
|