Iteration:

Als Iteration bezeichnet man eine wiederholte Anwendung einer Funktion zum Beispiel( f(x) = l×x ). Es wird mit einem Startwert x₀ begonnen, setzen den Wert x₀ in die Funktion ein und erhalten x₁ = f(x₀) = l×x₀. Nun wiederholt man den Vorgang mit dem dem Anfangswert von x₁, ist also x₂ = f(x₁) = l×x₁ = l²×x₀. So fortfahrend ergibt sich eine Folge von Zahlen x₀, x₁, x₂, ..... . Dies ist eine Iteration und bezeichnet die Menge {x₀, x₁, x₂, ...} als den Orbit O_xo (oder die Bahn) des Wertes x₀.
Bei einer komplexen Funktion entsteht in der komplexen Ebene eine Punktfolge: z₀, z₁ = f(z₀), x₂ = f(x₁), ...., z_k+1 = f(z_k). Damit läßt sich z_k als Funktion des Anfangswerts z₀ in der Form z_k = f^k(z₀) (kÎN₀) bezeichnen.
Solch eine Folge konvergiert (strebt) gegen einen Fixpunkt oder den Grenzwert ¥ an.

• Die Iteration an Beispielen: f(z) = kx+c

Die Variable c ist eine Konstante, diese bewirkt eine Verschiebung in die y-Richtung. Der Fixpunkt läßt sich über x = kx+c berechnen. ( x = 1/(1-k) ). Für alle Beispiele ist c = 0 und somit ist der Fixpunkt P(0/0). Dieser kann entweder abstoßend oder anziehend sein.

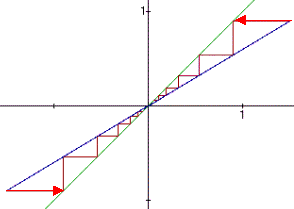
Die horizontale Gerade durch (x,f(x)) schneidet die Winkelhalbierende y = x im Hilfspunkt P. Die Vertikale durch P schneidet den Graphen im gesuchten Punkt (f(x),f(f(x))).

Anziehender Fixpunkt
k = 0,6	k = -0,6
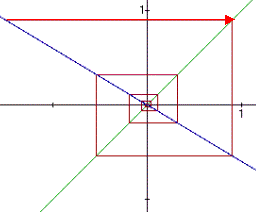
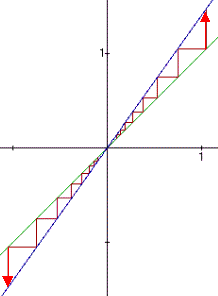
Abstoßender Fixpunkt
für k = 1,4	für k = -1,4

• Die Iteration an einem Beispiel für komplexe Zahlen: f(z) = z²

Zur Untersuchung des dynamischen Verhaltens der Folge z_k = f^k(z₀) wird folgende Darstellung benutzt:

Ist z₀ = re^ij der Startwert. Dann erhält man bei f(z₀) = (re^ij)² = r²e^2ij. Geometrisch ist es eine Drehstreckung.

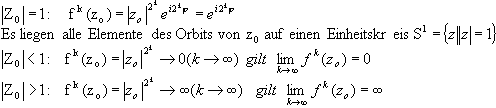
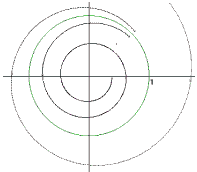
Aus z² = z ergeben sich die Fixpunkte 0 und 1.

Fixpunkte:

Ein Punkt x heißt U_z(x)Fixpunkt von f, wenn gilt f(x) = x ( somit gilt auch fⁿ(x) = x für nÎN).
Ein Fixpunkt der Periode k ist dann vorhanden, wenn gilt f^k(x) = x.
Ein echter Fixpunkt der Periode k liegt dann vor, wenn für alle j < k gilt f^j(x) ¹ x.
Ein Punt x heißt Fast-k-Fixpunkt von f, wenn gilt f^k+1(x) = f^k(x) aber fⁿ⁺¹(x) ¹ fⁿ(x) für alle n < k ( Spezialfall: Fast-0-Fixpunkt sind genau die Fixpunkte von f ).

• Anziehender Fixpunkt ( Attraktor )

Ein Fixpunkt heißt anziehender Fixpunkt ( Attraktor ), wenn es eine Umgebung U_z(x) gibt, so dass für alle yÎU_z(x) gilt: Der Grenzwert des Orbits O_y ist x.
Genauer:
Wenn gilt |f'(z)|<1, dann ist z ein Attraktor

• Abstoßender Fixpunkt ( Repellor )

Ein Fixpunkt heißt abstoßender Fixpunkt ( Repellor ), wenn es eine Umgebung U_z(x) gibt, so dass für alle yÎU_z(x) gilt: Der Grenzwert des Orbits O_y ist nicht aus U_z(x).
Genauer:
Wenn gilt |f'(z)|>1, dann ist z ein Repellor.

• Spezial Fälle

Wenn gilt |f'(z)| = 1, dann bezeichnet man z als indifferent.
Wenn gilt |f'(z)| = 0, dann bezeichnet man z als superanziehend.

• Der Punkt ¥ als anziehender Fixpunkt