Eine Zahl r>0 mit dieser Eigenschaft nennt man Fluchtschranke von f.
Sei f ein Polynom vom Grad ³2. Die Menge derjenigen
zÎC, für welche die Iterationsfolge (fk(z))
beschränkt bleibt, heißt ausgefüllte Julia
Menge von f:
K = K(f) = {zÎC|(fk(z)) ist beschränkt}
Der Rand von K(f) wird mit J(f) bezeichnet und heißt
Julia-Menge von f:
J(f): = dK(f)
Wenn keine Verwechslungen zu befürchten ist, wird K(f) auch als Julia-Menge
bezeichnet.
Außerhalb des Kreises um 0 mit dem Radius r strebt die Iterationsfolge
zk+1 = fk(zk) gegen ¥.
![]()
Eine Zahl r>0 mit dieser Eigenschaft nennt man Fluchtschranke von f.
Die wichtigste Fluchtschranke
Auf die Fluchtschranke r wird man geführt, wenn man nach einer möglichst
kleinen Zahl p>0 sucht, für die gilt:
|z| > p Þ |fc(z)| > p. Für
|z| > p erhält man:
|fc(z)| = |z2+c| ³
|z|2-|c| (Dreiecksungleichungen)
p2-|c| = p
und als positive Lösung von p2-p-|c| =
0 erhält man:
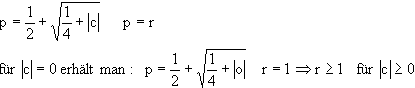
Die Fluchtschranke ist somit immer größer als
1
Sei nun |z| > r; dann erhält man:
|fc(z)| ³ |z|2-|c|
Þ |z|2- |c| = [r+(|z|-r)]2-|c|
= r2-|c|+2(|z|-r)+(|z|-r)2
r = r2-|c|
|fc(z)|-r ³ 2r(|z|-r) ³
2(|z|-r) für |z|>r
Wegen |fc(z)|>r gilt auch |fc2(z)|-r ³
2r(|fc(z)|-r)³ 22(|z|-r),
und damit für |z|>r
|fck(z)|³r+2k(|z|-r)
® ¥
(k®¥)
| Beispiel: |
| f(z) = z2+(4+31) |
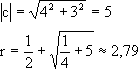 |
r = 2,79 ist somit die kleinste Fluchtschranke. Jedes r größer als 2,79 ist auch eine Fluchtschranke. Dies ist später für die grafische Wiedergabe wichtig.
Ist r eine Fluchtschranke von f, so gilt:
K(fc) liegt also ganz in der Kreisscheibe {z| |z| < r}
![]()
Die Julia-Menge wird nun mit Hilfe der Fluchtschranke definiert:
zÎK(f) Û
|fk(z)| £ r für alle kÎN0
K(fc) ist punktsymmetrisch zum Ursprung wenn gilt:
zÎK(fc) Û
-zÎK(fc)
fc(-z) = (-z)2+c = fc(z)
(fck)(-z) = (fc)k-1(fc(-z))
= (fc)k-1(fc(z)) = (fck)(z)
Die Folge (fck(-z)) ist also genau dann beschränkt,
wenn (fck(z)) beschränkt ist:
zÎK(fc) Û
-zÎK(fc)
 |
| K(fc) für c = 0.5+i0.5 |
![]()
![]()
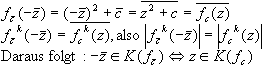
 |
 |
| K(fc) für c = 0.25+i0.53 | K(fc) für c = 0.25-i0.53 |