Beweis:
Mit c1 = c2+c und |c|>2 gilt
also |c1| > |c|.
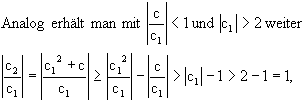
also |c2| > |c1|.
Man kann sagen, dass (zk) gegen den Punkt ¥ strebt für |c| > 2. Die Mandelbrot-Menge liegt also in der Kreisscheibe |c| £ 2.
Die Mandelbrot-Menge ist definiert:
Die ausgefüllte Julia-Menge K(fc) von fc(z)
= z2+c kann in Abhängigkeit
von c zusammenhängend sein oder nicht. Alle c-Werte, für die K(fc)
zusammenhängend ist, nennt man Mandelbrot-Menge.
M = {cÎC|K(fc)
zusammenhängend}
cÎM Û
K(fc) zusammenhängend Û
(fck(c)) beschränkt oder (fck(0))
beschränkt
Die bekannteste Figur der Mandelbrot-Menge ist das Apfelmänchen,
dabei ist z0 = 0. Für andere Startwerte
zeigen sich Bilder, die dem Apfelmänchen um so ähnlicher sind, je
kleiner |z0| ist.
Der Orbit von 0
Wegen fck(0) = c ist K(fc) genau dann zusammenhängend,
wenn 0ÎK(fc), wenn der Orbit von
0 beschrängt ist.
0, fc(0) = c, fc2(0) = fc(c) = c2+c,
fc3(0) = fc(c2+c) = c4+2c3+c2+c,....
Für die Folge (fck(z)) mit dem Anfangswert z =
c und |c| > 2 gilt:
![]()
Beweis:
Mit c1 = c2+c und |c|>2 gilt
![]()
also |c1| > |c|.
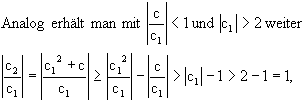
also |c2| > |c1|.
Man kann sagen, dass (zk) gegen den Punkt ¥
strebt für |c| > 2. Die Mandelbrot-Menge liegt also in der Kreisscheibe
|c| £ 2.
M schneidet die reelle Achse im Intervall [-2;1/4]
Beweis: c ist eine reelle Zahl. Im Fall c > 1/4 verläuft
die Parabel fc(z) = z2 + c ganz oberhalb der Winkelhalbierenden
und berührt die Winkelhalbierende für c = 1/4. Im Fall c £
1/4 ist ![]() der größere Fixpunkt von fc. Er bestimmt im Koordinatensystem
ein Quadrat mit den Seitenmitten (±z,0)
und (0;±z). Für
-2 £ c £ 1/4
liegt die Parabel fc(z) = z2 + c ganz in diesem Quadrat,
während sie für c < -2 das Quadrat nach unten durchstößt.
Für die Folgenglieder fck(0) gilt deswegen für
k®¥:
der größere Fixpunkt von fc. Er bestimmt im Koordinatensystem
ein Quadrat mit den Seitenmitten (±z,0)
und (0;±z). Für
-2 £ c £ 1/4
liegt die Parabel fc(z) = z2 + c ganz in diesem Quadrat,
während sie für c < -2 das Quadrat nach unten durchstößt.
Für die Folgenglieder fck(0) gilt deswegen für
k®¥:
| c > 1/4 | fck(0)®¥ | Þ c Ï M |
| -2 £ c £ 1/4 | fck(0)Î[-z,z] | Þ c Î M |
| c < -2 | fck(0)®¥ | Þ c Ï M |
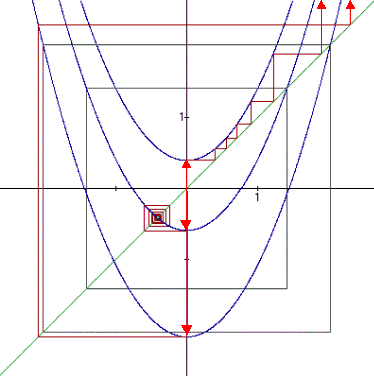
c1 = 0.3; c2 = -0.6; c3 = -2.1
fc1 und fc3®¥
für k®¥
Aus 0, fc(0) = c, fc2(0)
= fc(c) = c2+c, fc3(0) = fc(c2+c)
= c4+2c3+c2+c,.... erkennt man, dass
fck(0) = cn+an-1+...+a2c2+c
ein Polynom in c vom Grad n = 2k-1 mit reellen Koeffizienten ist.
Für den konjugierten komplexen Wert von fck (0) gilt
deshalb:
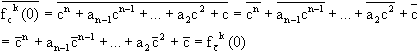
![]()