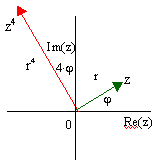Allgemeines:

Allgemein läßt sich nicht als reelle Zahl darstellen, denn ist keine reelle Zahl ( das Quadrat einer reellen Zahl ist immer positiv ). Die Quadratwurzel aus den negativen reellen Zahlen bilden also eine neue Art von Zahlen, man bezeichnet sie als imaginäre Zahlen.

Eine komplexe Zahl z ist ein geordnetes Paar (x,y) reeller Zahl.
z = (x,y) x = Re(z)R Realteil von z
y = Im(z)R Imaginärteil von z
Gleichheit z1 = (x1,y1) und z2 = (x2,y2)


Mit (1,0) = 1 als reeller Einheit (x,0) = x
(0,1) = i als imaginärer Einheit (0,y) = iy
Man bezeichnet mit i

daraus folgt eine Summendarstellung:
z = (x,y) = (x,0) = (0,y) = x+iy

Beispiel:

Gaußsche Zahlenebene:

Die komplexe Zahl z kann in einem rechtwinkligen Koordinatenssytem als Punkte der Ebene dargestellt werden (Gaußsche Zahlenebene).Die waagrechte Koordinatenachse (reelle Achse) entspricht den reellen Zahlen xR, die senkrechte Achse (imaginäre Achse) entspricht den imaginären Zahlen iyR.

Betrag:

Die Zahl |z| = heißt Betrag von z = x+iy. In der Gaußschen Zahlenebene stellt |z| den Abstand des Punktes z vom Nullpunkt dar.

Beispiel:
z = 1+2i hat den Betrag |z| =

Zusätzliche Betragsregeln:
 
( Dreiecksungleichungen )

Polarkoordinaten:

Eine Komplexe Zahl z = x+iy bzw. der Punkt P(x,y) ist durch die kartesische Koordinaten x,y festgelegt; z bzw. P(x,y) kann aber auch durch die Länge r des Ortsvektors und den Winkel j = arg(z) (Argument von z) bestimmt werden. Der Winkel schließt den und die reelle Achse ein.
Die Polarkoordinaten r,j von z = x+iy hängen mit dem kartesischen Koordinaten x,y wie folgt zusammen x = r cosj, y = r sin
r = |z| =
Für eine komplexe Zahl z = x+iy ergibt sich die folgende trigonometrische Darstellung:
z = |z|(cosj+isinj)
Dies wird auch als Eulersche Darstellung (L.Euler, 1707-1783) der komplexen Zahl z bezeichnet

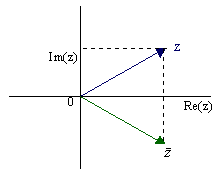
Konjugierte komplexe Zahl:

Bei einer komplexen Zahl z= x+iy wird das Vorzeichen des Imaginärteils invertiert, dabei erhält man die konjugierte komplexe Zahl = x-iy. Dies ist eine Spiegelung an der reellen Achse.
z = r (cosj+isinj) = r (cosj-isinj)

Es gelten folgende Regeln:

Geometrische Deutung

Addition:

Man addiert zwei komplexe Zahlen z1 = x1+iy1 und z2 = x2+iy2, indem man die Realteile und Imaginärteile der beiden Zahlen addiert und daraus die neue komplexe Zahl z bildet.
z = z1+z2 = (x1+x2)+i(y1+y2)

Beispiel:
z1 = 3+5i z2 = 2+3i
z = z1+z2 = (3+2)+i(5+3) = 5+8i

Die Subtraktion zweier komplexen Zahlen wird entsprechend der Addition durchgeführt:
z = z1-z2 = (x1-x2)+i(y1-y2)

Beispiel:
z1 = 3+5i z2 = 2+3i
z = z1-z2 = (3-2)+i(5-3) = 1+2i

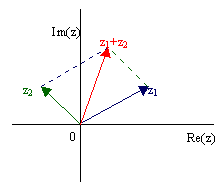
Geometrische Deutung

Die Addition komplexer Zahlen entspricht der Addition der Ortsvektoren nach der Parallelogrammregel.

Exponentialfunktion

Die Expotentialfunktion kann mit Hilfe der reellen Funktion ex, cosx und sinx wie folgt für komplexes z=x+iy (x,yÎR) definiert werden:
ez=ex(cosy+isiny)

Mit Hilfe der Additionstheoreme folgt ex1+x2 = ex1×ex2
Für reelles z = x (y = 0) ergibt sich aus ex(cos0+isin0) erneut der Wert ex der reellen Exponentialfunktion. Für rein imaginäres z = iy(x = 0) erhält man:
eiycosy+isiny

Damit kann die trigonometrische Darstellung einer komplexen Zahl wie folgt geschrieben werde:

z = |z|(cosj+isinj)=|z|eij

Multiplikation

Man multipliziert zwei komplexe Zahlen z1 = x1+iy1 und z2 = x2+iy2, indem man sie formel wie Binome multipliziert und beachtet, daß i2 = -1 ist.
z = z1×z2 = (x1+iy1)×(x2+iy2) = (x1x2-y1y2)+i(x1y2+x2y1)

Beispiel:
z1 = 3+5i z2 = 2+3i
z = z1×z2 = (6-15)+i(9+10) = -9+19i

Geometrische Deutung

Die Zahlen z1 = r1(cosj1+isinj1) und z2 = r2(cosj2+isinj2) werden miteinander multipliziert.

z = z1×z2 = r1(cosj1+isinj1)×r2(cosj2+isinj2) =
= r1r2(cosj1cosj2-sinj1sinj2+icosj1sinj2+icosj2sinj1)
Additionstheorem für die Kosinus-bzw. Sinusfunktion:
cosj1cosj2-sinj1sinj2 = cos(j1+j2)
cosj1sinj2+cosj2sinj1 = sin (j1+j2)

Þ z = z1×z2 = r1r2[cos(j1+j2)+isin (j1+j2)]
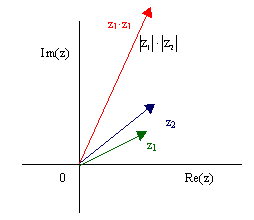
Man multipliziert komplexe Zahlen miteinander, indem man ihre absolute Beträge multipliziert und ihre Argumente addiert.

Andere Schreibweise:

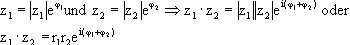
Beispiel:
z1 = 3(cos30°+isin45°) z2 = 4(cos45°+sin60°)
z = 12[cos(30°+45°)+isin(45°+60°)] = 12[cos75°+isin105°]

Division

Bei der Division von Komplexen Zahlen schreibt man den Quotienten der zu dividierenden komplexen Zahlen als Bruch und erweitert diesen so, dass der Nenner reell wird.
z1 = x1+iy1 und z2 = x2+iy2

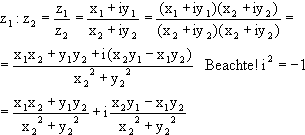
Dabei muß z2 = x2+iy2 ¹ 0 sein.

Beispiel:
z1 = 3+5i z2 = 2+3i

Geometrische Deutung

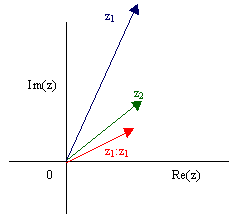
Man dividiert eine komplexe Zahl z1 durch eine komplexe Zahl z2, indem man den Betrag r1 von z1 durch den Betrag r2 von z2dividiert und das Argument j2von z2 vom Argument j1 von z1 subtrahiert.
z1 : z2 = r1(cosj1+isinj1) : r2(cosj2+isinj2)
z = z1 : z2 = (r1 : r2)[cos(j1-j2)+isin(j1-j2)]

Beispiel:
z1 = 3(cos30°+isin45°) z2 = 4(cos45°+sin60°)
z = 3/4[cos(30°-45°)+isin(45°-60°)] = 3/4(cos-15°+isin-15°)

 

Radizieren

Man zieht aus einer komplexen Zahl w die n-te Wurzel, indem man aus dem Betrag r der Zahl die n-te Wurzel zieht und das Argument j der Zahl durch n dividiert.

Dies ist der sogenannte Hauptwert von .
Außer dem Hauptwert von gibt es noch n-1 andere Werte für . Für irgendeine ganze Zahl k ist nämlich cos(j+2kp) = cosj und sin(j+2kp) = sinj.
Also gilt auch:

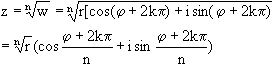
Für k = 0 erhält man daraus den Hauptwert.
Für k = 1,2,...,n-1 bekommt man n-1 verschiedene Nebenwerte.

Beispiel:
Die n-te Einheitswurzel z = .
Es ist in diesem Fall w = 1, also r = 1, j = 0° und k = 0,1,2,..,(n-1). (2kp = k360)
Man erhält also:

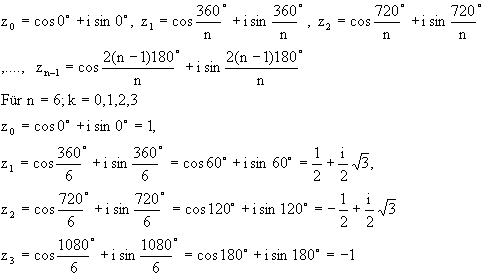Andere Schreibweise:

 Die Gleichung zn = w hat genau dann eine Lösung wenn w = 0 ist. Þz = 0
Im Fall w = |w|eij ¹ 0 besitzt zn = w genau n Lösungen:



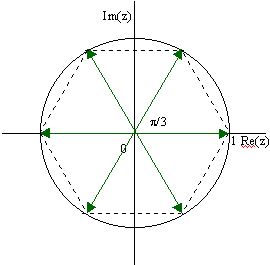
Die Lösungen bilden die Ecken eines regelmäßigen n-Ecks auf dem Kreis um 0 mit dem Radius

Im Fall zn = 1 erhält man daraus die |w| = 1 und j = arg(w) = 0 die n-ten Einheitswurzeln



n-te Einheitswurzel für n=6

Berechnung der Quadratwurzel mit dem Computer

Sei w ¹ 0 eine komplexe Zahl und liegt die trigonometrische Darstellung vor (w = |w|eij). So können ihre Quadratwurzeln leicht berechnet werden.



Ist w = u+iv gegeben, so können die Lösungen von z2 = w wie folgt in der Form z = x+iy angegeben werden.

  • Fall v = 0

    • Die Lösungen von z2 = u mit einer reellen, nicht notwendig positiven Zahl u ¹ 0 lauten:

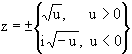
    Die Lösungen ( u>0 ) und ( u<0 ) sind die Quadratwurzeln positiver reeller Zahlen.

  • Fall v ¹ 0

    • z2 = (x+iy)2 = (x2-y2+i2xy) = u+iv Trennt man den Real und Imaginärteil, so erhält man die folgenden Gleichungen:
    x2-y2 = u
    2xy = v
    2xy = v Þ y = v/2x | v ¹ 0 und x ¹ 0
    y = v/2x in x2-y2 = u einsetzen

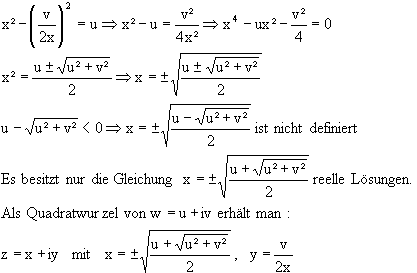
    Bemerkung:
    Bei der Berechnung der Quadratwurzel mit dem Computer kann es zu numerischen Problemen führen, wenn u negativ ist und v betragsmäßig sehr klein gegenüber u ist. Der Grund dafür sind die begrenzten Stellenanzeigen, die für die Darstellung einer Zahl verfügbar sind.

    Beispiel:
    u = -5 v = 0.002 (float-Variable 6 Stellen)

    Wegen den 6 Stellen ist 0,0000004 gleich 0. Dies hat zur Folge, dass x=0 und bei der Berechnung von y = v/2x kommt es zu einer Division durch 0. Man kann dies vermeiden, wenn man bei x2-y2 = u und 2xy = v im Fall u<0 die Rollen von x und y vertauscht.

    Potenzieren

    Man potenziert eine komplexe Zahl mit dem Exponenten n, indem man den Betrag r der Zahl mit n potenziert und das Argument j von z mit n multipliziert.
    zn = [r(cosj+isinj)]n = rn(cosj+isinj)n = rn[cos(nj)+isin(nj)]

    Beispiel:
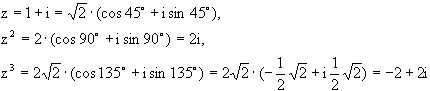